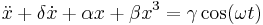Duffing equation

The Duffing equation is a non-linear second-order differential equation used to model certain damped and driven oscillators. The equation is given by

$\ddot{x} %2B \delta \dot{x} %2B \alpha x %2B \beta x^3 = \gamma \cos (\omega t)\,$

where the (unknown) function x=x(t) is the displacement at time t, 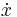$\dot{x}$ is the first derivative of x with respect to time, i.e. velocity, and 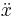$\ddot{x}$ is the second time-derivative of x, i.e. acceleration. The numbers 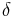$\delta$ , $\alpha$ , $\beta$ , $\gamma$ and $\omega$ are given constants.

The equation describes the motion of a damped oscillator with a more complicated potential than in simple harmonic motion (which corresponds to the case β=δ=0); in physical terms, it models, for example, a spring pendulum whose spring's stiffness does not exactly obey Hooke's law.

The Duffing equation is an example of a dynamical system that exhibits chaotic behavior. Moreover the Duffing system presents in the frequency response the jump resonance phenomenon that is a sort of frequency hysteresis behaviour.

Parameters

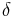$\delta$ controls the size of the damping (friction).
$\alpha$ controls the size of the restoring force.
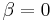$\beta$ controls the amount of non-linearity in the restoring force. If $\beta=0$ , the Duffing equation describes a damped and driven simple harmonic oscillator.
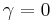$\gamma$ controls the amplitude of the periodic driving force. If $\gamma=0$ we have a system without driving force.
$\omega$ controls the frequency of the periodic driving force.

Methods of solution

In general, the Duffing equation does not admit an exact symbolic solution. However, many approximate methods work well:

Expansion in a Fourier series will provide an equation of motion to arbitrary precision.
The 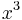$x^3$ term, also called the Duffing term, can be approximated as small and the system treated as a perturbed simple harmonic oscillator.
The Frobenius method yields a complicated but workable solution.
Any of the various numeric methods such as Euler's method and Runge-Kutta can be used.

In the special case of the undamped (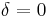 $\delta = 0$ ) and undriven ( 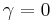$\gamma = 0$ ) Duffing equation, an exact solution can be obtained using Jacobi's elliptic functions.

External links

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›